02_求通项公式
总结 1
1 相邻两项 + 常数关系
遇到相邻两项 + 一个常数的关系。

2 相邻两项 + 一次函数关系

3 相邻两项 + 指数函数关系(2 种情况)
都是式子两边同除指数的 +1 次幂。

4 同除

5 取倒数

6 相邻三项,构造相邻两项的关系(或使用瞪眼法)
但注意,有时候不一定需要算出通项公式。有可能只是根据此关系式推导出某一项的奇偶性。比如这道题:

解






7 隔项问题
类似这种:

特征方程法
推导





总结

例题 1(裴波那切数列)

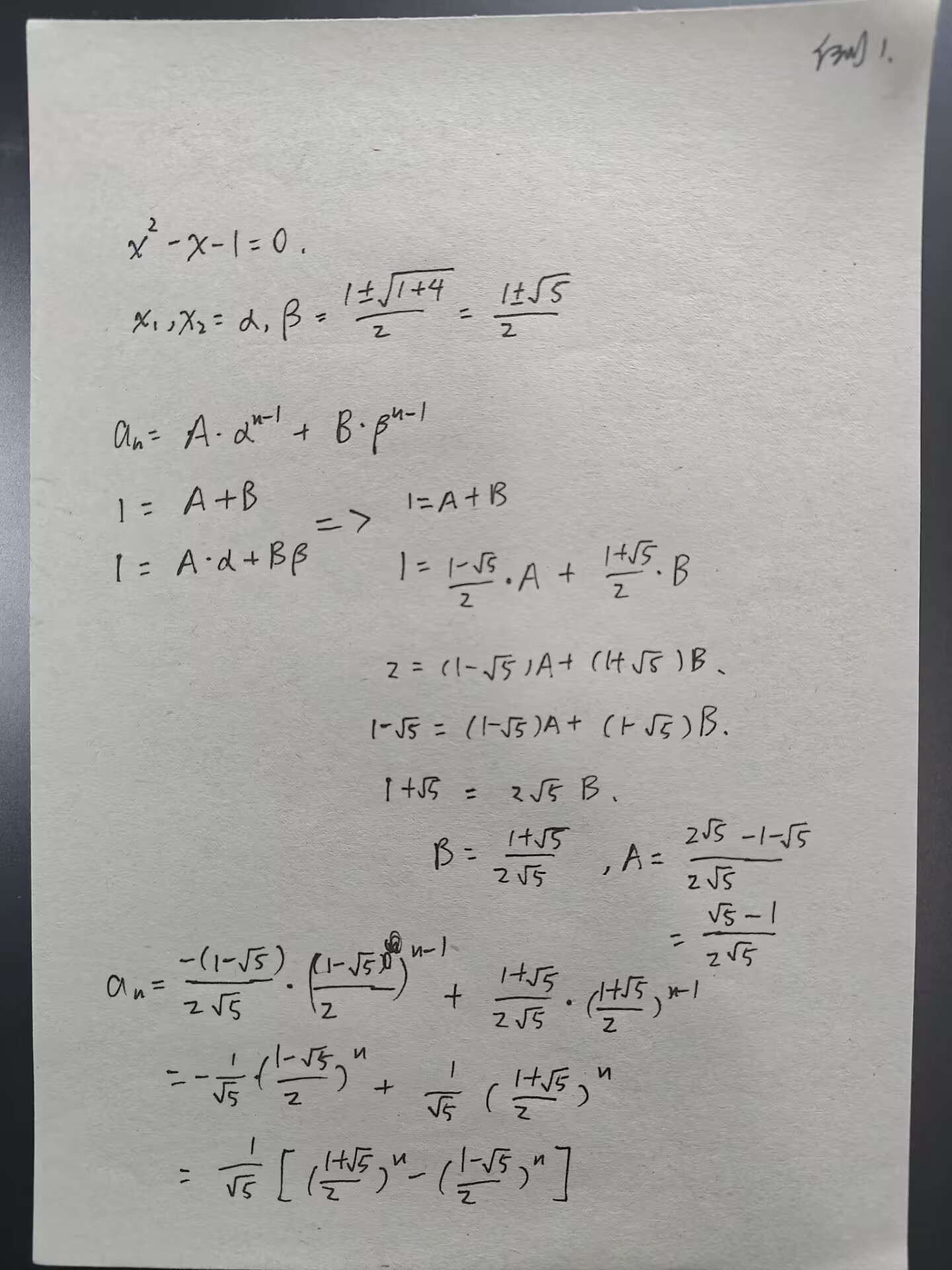
例题 2

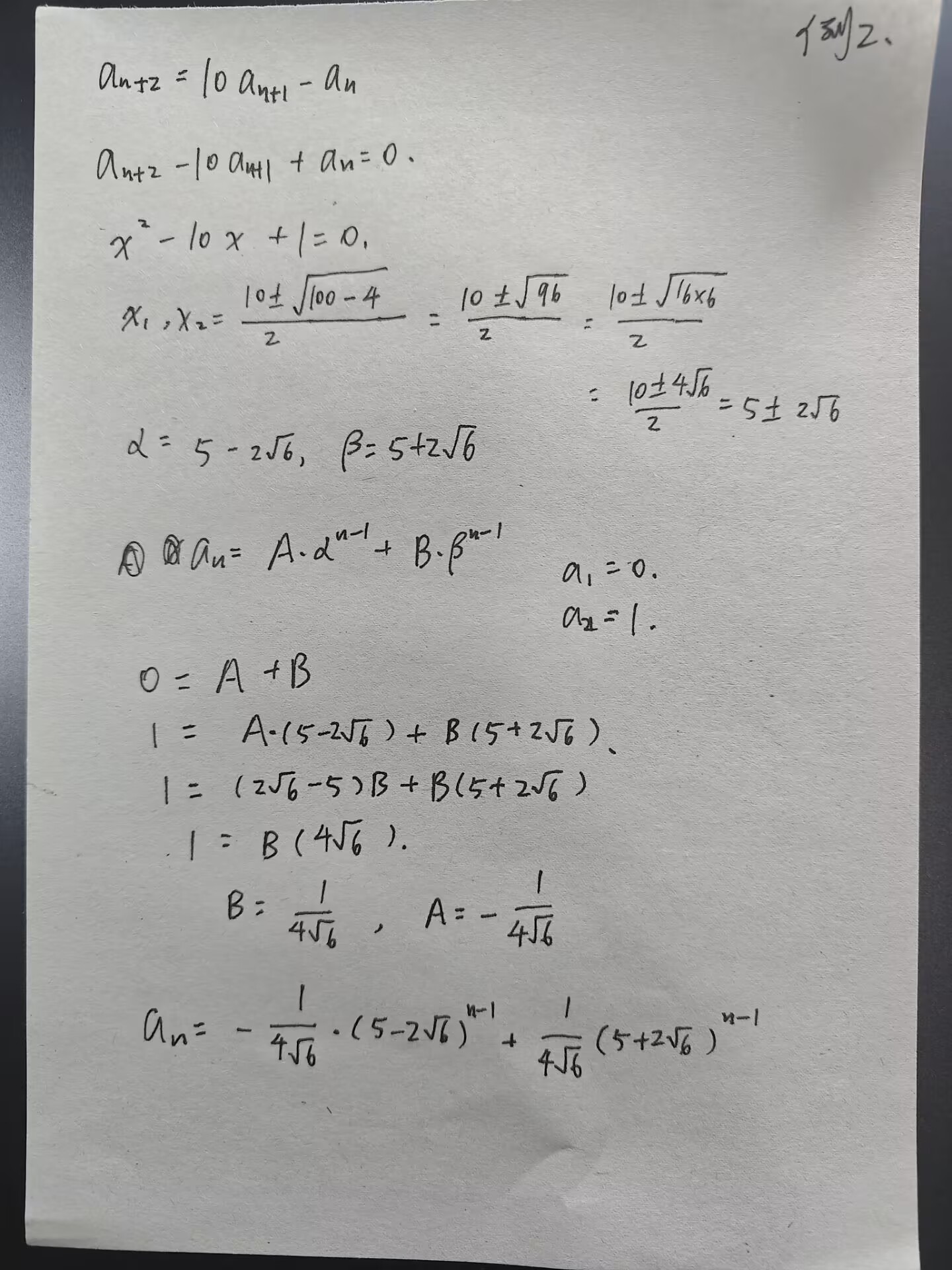
总结 2
相邻两项为函数形式(等差数列形式)
遇到数列的相邻两项之差为一个关于 n 的函数形式,使用累加法。
TIP
必须系数相同,即必须是
若系数不相同,则只能使用待定系数法。例如已知

举例:
有数列关系
TIP
如果题目给出的是
使用累加法,
左右两边同时相加,得
令
则
遇到指数也可以
遇见
但如果等式右边有指数比如
使用等比数列求和公式:
系数不是 1
如果遇到
比如
TIP
如果式子变为
两边同除
令
所以
等比数列形式
类似等比数列形式的题,都可以使用累乘法。
例子:
如有
例子:
例题:
解:
根据题目得,
所以
这时再使用累乘法,
两边各自相乘,得
有题目得, 错了,要根据通项公式来求。
由题目得,
所以
所以
当 n = 1 或 2 时,
所以
待定系数法
多了一个常数
什么时候用待定系数法呢?
例如有
例如有
假如我们在等比数列式子中加了一个常数 4,变成
如果我们使用累加法求解它的通项公式,会发现将
TIP
与之相对,如果系数相同。也不能使用待定系数法,而应使用累加或累乘法。
因为系数相同使用待定系数法,会发现设的系数会被约去,解不出来。
使用累乘法也约不掉。
这个时候我们就可以使用待定系数法,将它构造成一个等比数列。
第一步,我们设出一个常数
左边写成
即
如果我们令
我们将式子打开,变成
为了保证和原式子相同,我们就让
所以原式变为
假设
多了一个变量 C
比如
m 为系数
则设
多了一个变量 n
比如有题目
我们需要凑两个未知数
原始等于
化简得
所以可以将原始改写成
接下来的步骤就很简单了。
多了一个变量 n 的平法
比如题目给出条件
那么我们可以这样待定系数
多了一个指数
同理
变成
换元法
当一个题目中某个东西多次出现,或则有一个东西特别讨厌的时候(比如开根,分数),就可以考虑使用换元法。换元法不一定能解出题,但能给你多提供一个思路。
例如:
令
原式就变为
又是一个等比数列加一个常数项的体型,所以我们可以再使用待定系数法求解
总结 3




